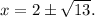The zeros for the given equation are A.
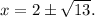
Explanation:
Step 1:
To solve for x in a polynomial equation, we use the formula
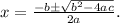
Here a is the coefficient of
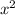 , b is the coefficient of
, b is the coefficient of
 and c is the coefficient of the constant term.
and c is the coefficient of the constant term.
In the given equation,
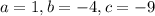 .
.
Step 2:
Substituting the values of a, b, and c in the equation, we get
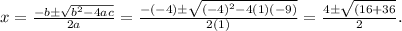
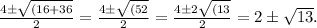
So the answer is option A.