Question

Two ropes are attached to a large ballon in a parade. The people holding the ropes are 40 feet apart,and the angle between the two ropes is 86 degrees. The angle of elevation of one rope is 42 degrees. How long is each rope..Step by Step explanation..Please ..Thanks.

Answer 1

Length of one side of rope is 31.5958 feet and length of other side is 26.828 feet

Explanation:

We are given distance between ropes = 40 feet

Angle between two ropes = 86 degrees

Angle of elevation of one rope = 42 degrees

We need to find the length of both ropes

First finding angle of elevation of 2nd rope:

180 - (86+42)=Angle of elevation of 2nd rope

Angle of elevation of 2nd rope = 52 degrees

Now finding sides of rope (see reference of figure attached)

Using Law of Sines:

`(Sin(C))/(c)=(Sin(B))/(b)`

Putting values of angle C and B and side c to find side

`(sin(86))/(40)=(sin(52))/(b) \\b(sin(86)=40(sin(52))`

`b(0.9976)=40(0.7880)\\b(0.9976)=31.52\\b=(31.52)/(0.9976)\\b=31.5958\,\,feet`

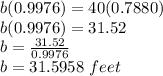
So, Length of side b is 31.5958 feet

Similarly finding length of side a

Using Law of Sines:

`(Sin(A))/(a)=(Sin(C))/(c)`

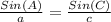
Putting values of angle C and B and side c to find side

`(sin(42))/(a)=(sin(86))/(40) \\40(sin(42)=a(sin(86))`

`40(0.6691)=a(0.9976)\\26.764=a(0.9976)\\a=(26.764)/(0.9976)\\a=26.828\,\,feet`

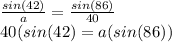
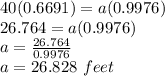
So, length of side a is 26.828 feet

Therefore, length of one side of rope is 31.5958 feet and length of other side is 26.828 feet