Question

Prove that 1 - sec x/1 + sec x is equal to cos x - 1/cos x + 1

Answer 1

Answer: See below

Explanation:

`(1-\sec x)/(1+\sec x)\quad =\quad (\cos x-1)/(\cos x+1)`

LHS --> RHS

Convert sec x to 1/(cos x):

`(1-(1)/(\cos x))/(1+(1)/(\cos x))`

Find a common denominator for the numerator and denominator:

`((\cos x)/(\cos x)-(1)/(\cos x))/((\cos x)/(\cos x)+(1)/(\cos x))\quad = \quad ((\cos x-1)/(\cos x))/((\cos x+1)/(\cos x))`

Eliminate the denominators:

`\quad (\cos x-1)/(\cos x+1)`

LHS = RHS so identity is proven.

Answer 2

`(1-secx)/(1+secx)` =
`(cosx - 1)/(cosx + 1)`

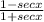Explanation:

We are to prove that 1 - sec x/1 + sec x is equal to cos x - 1/cos x + 1

To do this, we need to know that secx= 1/cosx

from the question given (1-secx) ÷ (1+secx)

Lets first simplify (1-secx)

1-secx = 1 - 1/cosx =
`(cosx - 1)/(cosx)`

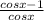
Also we will go ahead and simplify (1+secx)

1 + secx = 1 + 1/cosx =
`(cosx + 1)/(cosx)`

`(1-secx)/(1+secx)` =
`(cosx - 1)/(cosx)` ÷
`(cosx + 1)/(cosx)`

=
`(cosx - 1)/(cosx)` ×
`(cosx)/(cosx + 1)`

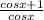
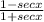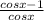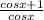
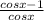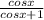
(The cosx at the numerator will cancel-out the cosx at the denominator)

=
`(cosx - 1)/(cosx + 1)`

`(1-secx)/(1+secx)` =
`(cosx - 1)/(cosx + 1)`

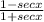Hence proved.