Question

he length of a rectangle is increasing at a rate of 3 cm/s and its width is increasing at a rate of 9 cm/s. When the length is 13 cm and the width is 5 cm, how fast is the area of the rectangle increasing?

Answer 1

The area of the rectangle increases are the rate of 132 cm²/s when the length is 13 cm and the width is 5 cm

Explanation:

The area of the rectange is given by the following formula:

`A = l*w`

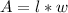
In which A is the area, measured in cm², l is the lenght and w is the width, both measured in cm.

The length of a rectangle is increasing at a rate of 3 cm/s and its width is increasing at a rate of 9 cm/s.

This means that
`(dl)/(dt) = 3, (dw)/(dt) = 9`

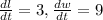
When the length is 13 cm and the width is 5 cm, how fast is the area of the rectangle increasing?

We have to find
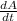`(dA)/(dt)` when
`l = 13, w = 5`

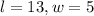
Applying implicit differentitiation:

We have three variables(A, l, w). So

`A = l*w`

`(dA)/(dt) = l(dw)/(dt) + (dl)/(dt)w`

`(dA)/(dt) = 13*9 + 3*5`

`(dA)/(dt) = 132`

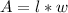
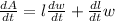
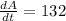
The area of the rectangle increases are the rate of 132 cm²/s when the length is 13 cm and the width is 5 cm