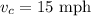Question

A boat travels upstream for 360 miles in 4 hours and returns in 3 hours traveling downstream in a local stream of water. What is the rate of the boat in still water and the rate of the current?

Answer 1

Rate of boat in still water = 105 mph

Rate of current = 15 mph

Step-by-step explanation:

Let the speed of the boat in still water be
`v_b`.

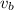Let the speed of the current be
`v_c`.

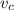When the boat goes upstream, it moves against the current. Hence, its velocity will be relative to that of the current. This is given by 360/4 = 90 mph.

This relative velocity is the difference between the speed of the boat in still water and that of the current:

`v_b - v_c = 90`

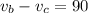
In the downstream, the boat moves with the current. The resultant velocity is the sum of the velocities of boat in still water and current.

`v_b+v_c = 360/3 =120`

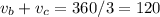
Solving both equations simultaneously by elimination method,

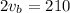`2v_b = 210` (adding both equations)

`v_b = 105\text{ mph}`

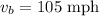
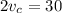`2v_c = 30` (subtracting the first from the second equation)

`v_c =15\text{ mph}`