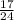Question

Jon's closet has 3 black shirts, 8 blue shirts, 6 black pants and 7 blue pants. He wants to determine the probability of selecting a black piece of clothing OR a shirt from his closet. He solves the probability this way: P(black piece of clothing or a shirt) = P(black piece of clothing) + P(shirt) = 9/24+11/24=20/24=56 Did he solve it correctly?

Answer 1

No the solution is incorrect.

p(black piece of clothing or a shirt) =
`(17)/(24)`

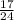
Explanation:

given

No. of black shirts = 3

No. of blue shirts = 8

No. of black pants = 6

No. of blue pants = 7

Total no. of clothing = 24

No. of black piece of clothing = 3+6 = 9

No. of shirts = 3+8 = 11

Problem is : Probability p(black piece of clothing or a shirt)

In In probability 'or' means that the outcome must satisfy one condition or other condition or both. We have to apply addition rule: when two events A and be are mutually exclusive, the probability that A or B will occur is given by

P(A U B) = P(A) +P(B)

Also when two events A and be are non-mutually exclusive, the probability that A or B will occur is given by

P(A U B) = P(A) +P(B) - P(A ∩ B)

The given problem falls under non-mutually exclusive

Hence

p(black piece of clothing or a shirt) = p(black piece of clothing) +p(a shirt) - p(black piece of clothing and a shirt)

[Here p(black piece of clothing and a shirt) is no of black shirts/total no of clothing]

p(black piece of clothing or a shirt) =
`(9)/(24)` +
`(11)/(24)` -
`(3)/(24)`

=
`(17)/(24)`

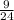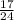
Hence p(black piece of clothing or a shirt) =
`(17)/(24)`