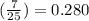The probability of selecting a random student who is enrolled in both the courses is 0.280.
Explanation:
Here, the total number of freshman in the university = 500
The number of students enrolled in Economics = n(E) = 323
The number of students enrolled in Mathematics = n(M) = 205
The number of students enrolled in Both Economics and math
= n(E∩M ) = 140
Let F : Event of selecting a student who is enrolled in both the courses
So, from the given data:
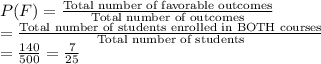
So, the probability of selecting a random students who is enrolled in both the courses is