Question

One end of an insulated metal rod is maintained at 100 ∘C and the other end is maintained at 0.00∘C by ice–water mixture. The rod has a length of 55.0 cm and a cross-sectional area of 1.00 cm2. The heat conducted by the rod melts a mass of 5.00 g of ice in a time of 10.0 min. Find the thermal conductivity k of the metal?

Answer 1

153.0815W/m.K

Step-by-step explanation:

Heat transferred in phase is changed is expressed as:

`Q=\pm mL` (m-mass, Q-heat, L-Latent heat of phase change)

Latent heat is the heat required to change the phase of 1kg of the material.

#The rate of heat flow(by conduction) per unit time:

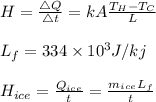`H=(\bigtriangleup Q)/(\bigtriangleup t)=kA(T_H-T_C)/(L)\\\\L_f=334*10^3J/kj\\\\H_(ice)=(Q_(ice))/(t)=(m_(ice)L_f)/(t)` #Heat flowing through melting ice.

`H_(ice)=(5.0*10^-^3kg)334*10^3J/kg))/(10*60s)\\\\=2.7833J/s`

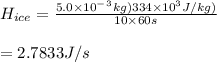
To solve for k:

`H=(\bigtriangleup Q )/(\bigtriangleup t)\\\\=kA(T_H-T_C)/(L)`
`H=(\bigtriangleup Q )/(\bigtriangleup t)\\\\=kA(T_H-T_C)/(L)`
`H=(\bigtriangleup Q )/(\bigtriangleup t)\\\\=kA(T_H-T_C)/(L)\\\\k=(H)/(A(T_H-T_C)/(L))=(HL)/(A(T_H-T_C))`

`=((2.7833J/s* 0.55))/(1.00*10^-^4m^2* 100K)\\\\=153.0815W/m.K`

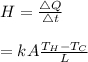
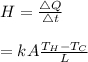
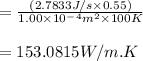
The thermal conductivity k of the metal is 153.0815W/m.K