Question

Two heat engines operating on Carnot cycles are arranged in series. The first engine A receives heat at 927 C and rejects heat to reservoir at temperature T. The second engine B receives the heat rejected by the first engine, and in turn rejects heat to a reservoir at 27 C. Calculate the temperature T, in C, for the situation where:

a. the work outputs of the two engines are equal.
b. the efficiencies of the two engines are equal.

Answer 1

The answers to the questions are;

a. The temperature T where the work outputs of the two engines are equal is 700 K.

b. The temperature T where the efficiencies of the two engines are equal is 600 K.

Step-by-step explanation:

To solve the question, we note that

T₁ = 927 °C = 1200.15 K

T₃ = 27 °C = 300.15 K

We are required to calculate T the output temperature of the first engine

(i) When the work outputs of the two engines are equal we have

We put the the work output to be = W

Whereby the work done by the first engine is given by the work done in Carnot cycle which is -∑ W = ∑ Q

Then A receives heat at Q₁ at 1200.15 K and rejects heat at Q₂ at T K therefore W
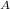`_A` = Q₁ - Q₂

Similarly B receives heat at Q₂ at T K and rejects heat at Q₃ at 300.15 K

therefore W
`_B` = Q₂ - Q₃

Where W
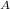`_A` = W
`_B`

Q₁ - Q₂ = Q₂ - Q₃ Dividing both sides by Q₁, we have

(Q₁ - Q₂)/Q₁ = (Q₂ - Q₃)/Q₁

1 - Q₂/Q₁ = Q₂/Q₁ - Q₃/Q₁

1 - T/T₁ = T/T₁ -T₃/T₁

Which gives 1+T₃/T₁ = 2 ×T/T₁

T = T₁ /2×(1+T₃/T₁ ) = 1200.15/2×(1+300.15/1200.15) = 750.15 K

T = 750.15 K ≈ 750 K

b. When the efficiencies of the two engines are equal we have

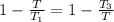`1 - (T_)/(T_1) = 1 - (T_3)/(T_)` which gives

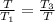`(T_)/(T_1) = (T_3)/(T_)` therefore T² = T₃×T₁ = (1200.15 K) × (300.15 K) = 360225.0225 K²

T =
`\sqrt{360225.0225 K^(2) }` = 600.187 K ≈ 600 K

Answer 2

(a) 477°C

(b) 327°C

Step-by-step explanation:

The solution is explained or solved in the attach document.