Answer:
a) μ = 0.1957 , b) ΔK = 158.8 J , c) K = 0.683 J
Step-by-step explanation:
We must solve this problem in parts, one for the collision and the other with the conservation of energy
Let's find the speed of the wood block after the crash
Initial moment. Before the crash
p₀ = m v₁₀ + M v₂₀
Final moment. Right after the crash
pf = m
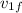 + M v_{2f}
+ M v_{2f}
The system is made up of the block and the bullet, so the moment is preserved
p₀ = pf
m v₁₀ = m v_{1f} + M v_{2f}
v_{2f} = m (v₁₀ - v_{1f}) / M
v_{2f} = 4.5 10-3 (400 - 190) /0.65
v_{2f} = 1.45 m / s
Now we can use the energy work theorem for the wood block
Starting point
Em₀ = K = ½ m v2f2
Final point
Emf = 0
W = ΔEm
- fr x = 0 - ½ m v₂₂2f2
The friction force is
fr = μN
With Newton's second law
N- W = 0
N = Mg
We substitute
-μ Mg x = - ½ M v2f2
μ = ½ v2f2 / gx
Let's calculate
μ = ½ 1.41 2 / 9.8 0.72
μ = 0.1957
b) let's look for the initial and final kinetic energy
K₀ = 1/2 m v₁²
K₀ = ½ 4.50 10⁻³ 400²
K₀ = 2.40 10² J
Kf = ½ 4.50 10⁻³ 190²
Kf = 8.12 10¹ J
Energy reduction is
K₀ - Kf = 2.40 10²- 8.12 10¹
ΔK = 158.8 J
c) kinetic energy
K = ½ M v²
K = ½ 0.650 1.45²
K = 0.683 J