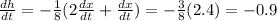Question

A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks along the x-axis from the spotlight toward the building at a speed of "2.4" m/s, which is taken as the given dx/dt, how fast is the length of his shadow on the building decreasing when he is 4 m from the building

Answer 1

`(dh)/(dt)= -0.9 m/s`

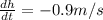
Explanation:

Let h be the length of the shadow. Consider the figure attached. Since the triangles are similar, we have the following relation.

`(2)/(h)= (x)/(12-x)`

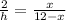
Which leads to the equation
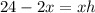`24-2x=xh`. Differentiating this equation with respect to x leads to

`-2(dx)/(dt)= (dx)/(dt)h+(dh)/(dt)x`

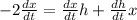
We want to find the rate of change for h, then

`(dh)/(dt) = -(1)/(x)(2(dx)/(dt)+(dx)/(dt)h)`

Using the relation we found, we have that
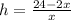`h= (24-2x)/(x)`. Now, we now that the man is 4 m away of the building. That is, that x = 8. Then, h = 1.

So, replacing this value in the equation we have

`(dh)/(dt) = -(1)/(8)(2(dx)/(dt)+(dx)/(dt))= -(3)/(8)(2.4)= -0.9`