Here is the full question
A snack food company wishes to have a cylinder package for it's almond and cashew mix. The cylinder must contain 120 cm³ worth of product. The base and sides will cost $.01 per cm2 to produce but the top, which is plastic and resealable, will cost $.02 per cm2 to produce. What should the dimensions be to minimize cost?
Answer:
The radius and height are both dimension in the cylinder; in order to minimize the cost
radius = 2.515 cm
height = 18.93 cm
Explanation:
We denote the radius of the cylinder to be = r
and the height of the cylinder = h
The volume of a cylinder is known to be = πr²h
Also, from the question; we are also told that the cylinder contains 120 πcm³
i.e πr²h = 120π
Dividing both sides with π; we have:
r²h = 120
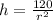
The base and sides will cost $.01 per cm² to produce
Total cost of the base and side
 = 0.01 ( πr² + 2πrh)
= 0.01 ( πr² + 2πrh)
but the top, which is plastic and resealable, will cost $.02 per cm² to produce.
i.e
cost of the top cylinder
 = 0.02 ( πr²)
= 0.02 ( πr²)
Overall Total cost =
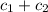
= 0.01 ( πr² + 2πrh) + 0.02 ( πr²)
= 0.01 πr² + 0.02 πrh + 0.02 πr²
=
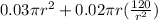
=
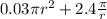
Taking the differentiation to find the radius dimension to minimize cost; we have:
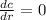 ⇒
⇒
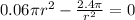
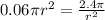

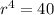
![r = \sqrt[4]{40}](https://img.qammunity.org/2021/formulas/mathematics/college/iseiorp9an2mks8kksos8v9lb5kgjqlqyp.png)
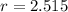 cm
cm
However,
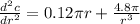
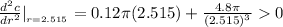
Therefore; we can say that the cost is minimum at r = 2.515 since it is positive.
To determine the height ; we have:
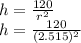
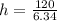
h = 18.93 cm