Answer:
The flow is super critical
Step-by-step explanation:
The average velocity of flow is given, V= 1.3 m / s.
Depth of flow, y= 2 cm= 0.02 m
Suppose the flow is in a small rectangular channel.
The number Froude,
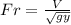 .
.
The strength of gravity, g= 9.81 m / s^2,
Replaces the identified values.
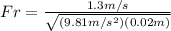
= 2.935
We recognize that the open channel flow is super critical, if the Froude number, Fr > 1.
And the flow is super critical.