Question

An insurance company estimates 45 percent of its claims have errors. The insurance company wants to estimate with 99 percent confidence the proportion of claims with errors. What sample size is needed if they wish to be within 5 percent of the actual

Answer 1

We need a sample size of at least 657.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

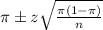
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is given by:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

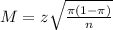
45 percent of its claims have errors.

So
`\pi = 0.45`

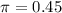
99% confidence level

So
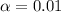`\alpha = 0.01`, z is the value of Z that has a pvalue of
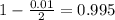`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

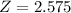What sample size is needed if they wish to be within 5 percent of the actual

This is a sample size of at least n, in which n is found when M = 0.05.

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.05 = 2.575\sqrt{(0.45*0.55)/(n)}`

`0.05√(n) = 1.28`

`√(n) = (1.28)/(0.05)`

`√(n) = 25.62`

`√(n)^(2) = (25.62)^(2)`

`n = 656.4`

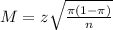
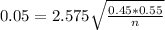
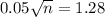
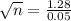
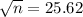
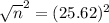
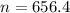
We need a sample size of at least 657.