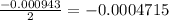Question

A circular copper bar with diameter d 5 3 in. is subjected to torques T 5 30 kip-in. at its ends. Find the maximum shear, tensile, and compressive stresses in the tube and their corresponding strains. Assume that G 5 6000 ksi.

Answer 1

Maximum shear stress= 5.66 ksi

Maximum tensile stress= 5.66 ksi

Maximum compressive stress=-5.66 ksi

Maximum shear strain=0.000943

Maximum tensile strain= 0.0004715

Maximum compressive strain= -0.0004715

Step-by-step explanation:

Answer 2

Maximum shear stress= 5.66 ksi

Maximum tensile stress= 5.66 ksi

Maximum compressive stress=-5.66 ksi

Maximum shear strain=0.000943

Maximum tensile strain= 0.0004715

Maximum compressive strain= -0.0004715

Step-by-step explanation:

For acircular bar, the maximum shear stress will be given by

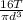`\frac {16T}{\pi d^(3)}` where d is the diameter and T is torque.

By substituting 30 kip-in for torque and 3 in for d then

Maximum shear stress=
`\frac {16*30}{\pi *3^(3)}\approx 5.66 ksi`

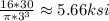
Also, the maximum tensile and compressive stresses will be 5.66 ksi and -5.66 ksi respectively.

The maximum shear strain will be given by stress divided by modulus of elasticity, in this case 6000 G

Maximum shear strain will be
`\frac {5.66}{6000}\approx 0.000943`

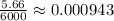
The maximum tensile strain will be the above divided by 2 whereas the maximum compressive strain will be negative of tensile strain hence
`\frac {0.000943}{2}=0.0004715`

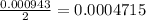
Maximum compressive strain will be
`\frac {-0.000943}{2}=-0.0004715`