
Divide through the ODE by the largest power of
 , assuming
, assuming
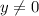 :
:

By the chain rule,
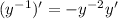 . So substitute
. So substitute
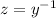 and
and
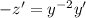 to get
to get

which is linear in
 . Multiply both sides by
. Multiply both sides by
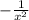 :
:
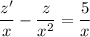
Now the left side is the derivative of a product, so we can condense this as
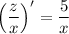
Integrate both sides with respect to
 :
:

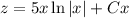
Solve for
 :
:
