Question

Find the length arc of DB. Leave your answer in terms of pi.

Answer 1

Length of arc DB = 14 π feet

Solution:

Radius AB = 18 feet

DC is the diameter of the circle.

∠CAB = 40°

Sum of the adjacent angles in a straight line = 180°

m∠DAB + m∠CAB = 180°

m∠DAB + 40° = 180°

Subtract 40° from both sides.

m∠DAB = 140°

To find the length of arc DB:

`$\text{Arc length} =2 \pi r\left((\theta)/(360)\right)`

`$ =2 \pi * 18\left((140^\circ)/(360)\right)`

`$ =2 \pi \left((140^\circ)/(20)\right)`

=
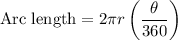
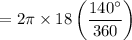
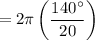
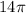`14\pi` feet

Length of arc DB = 14 π feet