Length of arc DB = 14 π feet
Solution:
Radius AB = 18 feet
DC is the diameter of the circle.
∠CAB = 40°
Sum of the adjacent angles in a straight line = 180°
m∠DAB + m∠CAB = 180°
m∠DAB + 40° = 180°
Subtract 40° from both sides.
m∠DAB = 140°
To find the length of arc DB:
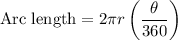
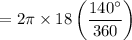
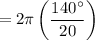
=
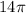 feet
feet
Length of arc DB = 14 π feet