Question

A ball has been thrown into the air its distance from the ground is given by the function s(t)=-16t^2+96t+100

where t is measured in seconds and s is measured in feet. At what time the velocity change from positive to negative {} seconds.

Answer 1

For t=3 sec the velocity change from positive to negative

Explanation:

we have

`s(t)=-16t^2+96t+100`

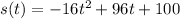
This is the equation of a vertical parabola open downward (the leading coefficient is negative)

where

s(t) is the distance in feet

t is the time in seconds

We know that

To find out when the velocity change from positive to negative, we need to determine the turning point of the quadratic equation

The turning point of the quadratic equation is the vertex

so

Convert the quadratic equation into vertex form

`s(t)=-16t^2+96t+100`

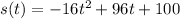
Factor -16

`s(t)=-16(t^2-6t)+100`

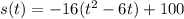
Complete the square

`s(t)=-16(t^2-6t+9)+100+144`

`s(t)=-16(t^2-6t+9)+244`

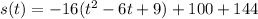
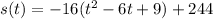
Rewrite as perfect squares

`s(t)=-16(t-3)^2+244`

The vertex is the point (3,244)

therefore

For t=3 sec the velocity change from positive to negative