Question

In recent years the state of California issued license plates using a combination of one letter of the alphabet followed by four digits, followed by another three letters of the alphabet. How many different license plates can be issued using this configuration (without repetition)

Answer 1

1,808,352,000 different license plates can be issued using this configuration

Explanation:

The order is important. For example, if the letters are EM, it is already a different plate than if the letters were ME. So we use the permutations formula to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

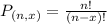
Four letters

In the alphabet, there are 26 letters. In the place, there are 4. So permutations of 4 from a set of 26.

`P_((26,4)) = (26!)/(4!) = 358800`

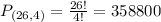
Four digits

There are 10 digits. In the plate, there are four. So permutations of 4 from a set of 10

`P_((10,4)) = (10!)/(6!) = 5040`

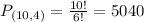
Total

Multiplying these values

358800*5040 = 1,808,352,000

1,808,352,000 different license plates can be issued using this configuration