Answer:
Here, the given equations,
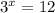 and
and
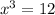
Similarity: In both equations there is only one variable ( i.e. x)
Difference:
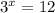 is an exponential equation while
is an exponential equation while
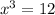 is a polynomial equation.
is a polynomial equation.
Now, when we solve an exponential equation we take log in both sides of the equation as follows:
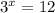

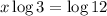 ( ∵
( ∵
 )
)
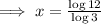
Hence, the solution of the equation
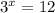 is
is
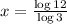 .
.
While, when we solve a polynomial we find the roots as follows:
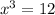
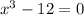

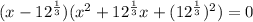
By zero product property,
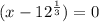 or
or
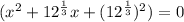
If
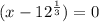 , then
, then

If
 ,
,
Then, by quadratic formula,
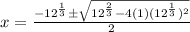
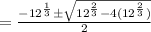
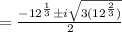
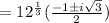
Hence, the solutions of the equation
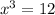 are
are
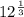 ,
,
 and
and
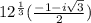 .
.