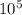Question

Water at 20 °C is flowing with velocity of 0.5 m/s between two parallel flat plates placed 1 cm apart. Determine the distances from the entrance at which the velocity and thermal boundary layers meet.

Answer 1

Therefore, the distance from the entrance at which the velocity and thermal boundary layer meets is x = 0.516 m,
`x_(r)` = 1.889 m

Step-by-step explanation:

The value for the property of water was obtained at 20° C from the table.

ρ = 998 Kg/
`m^(3)`

μ = 1.002 ×
`10^(-3)` Kg/m.s

Pr = 7.01

The waters kinematic viscosity is calculated at 20° C using the relation.

`v=(\mu)/(\rho)`

`v=(1.002 * 10^(-3))/(998)`

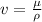
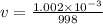
v = 1.004 ×
`10^(-6)`
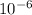
`m^(2)`/s

The thickness of thermal boundary layer is calculated using the relations.

`\delta_(r)=(y)/(2)`

`\delta_(r)` =
`(0.01)/(2)`

`\delta_(r)` = 0.005 m

`\delta_(v)` =
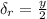
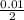
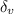`\delta_(r)` = 0.005 m

Predict the flow is laminar,

The formula for the thickness of the velocity boundary layer is

`\delta_(v)=\frac{4.91}{\sqrt{(V)/((v x))}}`

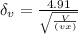
The entrance by the distance was calculated in which the velocity boundary layer meets as shown.

The equation is rearranged.

`\sqrt{((v x))/(V)}=(\delta_(v))/(4.91)`

Square Both the equations:

`(\sqrt{((v x))/(V)})^(2)=\left((\delta_(v))/(4.91)\right)^(2)`

`((v x))/(V)=\left((\delta_(v))/(4.91)\right)^(2)\\`

`x=(V)/(v)\left((\delta_(v))/(4.91)\right)^(2)`

`x=(0.5)/(1.004 * 10^(-6))\left((0.005)/(4.91)\right)^(2)`

=
`0.498 * 10^(6) * 1.036 * 10^(-6)`

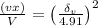
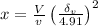
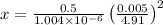
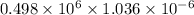
x = 0.516 m

The formula for the thermal boundary layers thickness is

`\delta_(r)` =
`\frac{4.91}{Pr^(1/3)\sqrt{(v)/(vx_(r) ) } }`

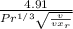
The entrance by the distance was calculated in which the velocity boundary layer meets as shown.

`\sqrt{(\left(v x_(r)\right))/(V)}=\frac{\delta_(r) * \mathrm{Pr}^(1 / 3)}{4.91}`

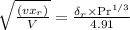
Square Both the equations:

`(\sqrt{(\left(v x_(r)\right))/(V)})^(2)=\left(\frac{\delta_(r) * \mathrm{Pr}^(1/3)}{4.91}\right)^(2)`

`(\left(v x_(r)\right))/(V)=\left((\delta_(r))/(4.91)\right)^(2)\left(\mathrm{Pr}^(1/3)\right)^(2)\\`

`x_(r)=(V)/(v)\left((\delta_(r))/(4.91)\right)^(2)\left(\mathrm{Pr}^(2 / 3)\right)`

`x_(r)=(0.5)/(1.004 * 10^(-6))\left((0.005)/(4.91)\right)^(2)(7.01)^(2 / 3)`

`=0.498 * 10^(6) * 1.036 * 10^(-6) * 3.662`

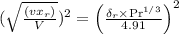
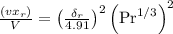
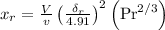
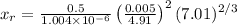
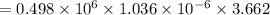
`x_(r)` = 1.889 m

The Reynolds number value is calculated, x = 0.516 m.

`\mathrm{Re}=(V x)/(v)`

`\mathrm{Re}=(0.5 * 0.516)/(1.004 * 10^(-6))`

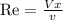
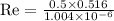
Re = 2.57 ×
`10^(5)` < 5 ×
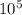`10^(5)`