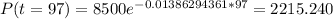Question

A quantity with an initial value of 8500 decays exponentially at a rate such that the

quantity cuts in half every 5 decades. What is the value of the quantity after 97 years,

to the nearest hundredth?

Answer 1

`4250 = 8500 e^(50 k)`

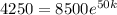
And we can divide both sides by 8500 and we got:

`(1)/(2) = e^(50 k)`

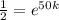
And we can solve for k using natural log

`k = (ln((1)/(2)))/(50)= -0.0138629`

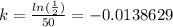
And we have the model give by:

`P(t) = 8500 e^(-0.01386294361 t)`

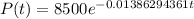
And if we replace t =97 we got:

`P(t=97) = 8500 e^(-0.01386294361 *97)= 2215.240`

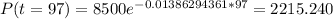
Explanation:

For this case we can use the proportional model given by:

`(dP)/(dt)= kP`

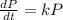
And we can rewrite the expression like this:

`(dP)/(P) = k dt`

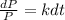
If we integrate both sides we got:

`ln P = kt +C`

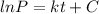
If we apply exponentials in both sides we got:

`P = e^(kt +C)`

And we can rewrite the expression like this:

`P(t) = P_o e^(kt)`

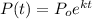
Where P represent the population and t the time in years since the starting value

For this case we have that
`P_o = 8500`

And after t = 5*10 = 50 years the value is the half or 8500/2 = 4250

So we can use this condition and we have:

`4250 = 8500 e^(50 k)`

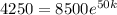
And we can divide both sides by 8500 and we got:

`(1)/(2) = e^(50 k)`

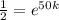
And we can solve for k using natural log

`k = (ln((1)/(2)))/(50)= -0.0138629`

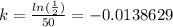
And we have the model given by:

`P(t) = 8500 e^(-0.01386294361 t)`

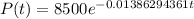
And if we replace t =97 we got:

`P(t=97) = 8500 e^(-0.01386294361 *97)= 2215.240`