Question

With your team, find a sequence of transformations that will transform figure C to become figure D​

Answer 1

Answer:Yes

Step-by-step explanation:Yes

Answer 2

Answer: Dilation of 1/2, translation 5 1/2 left and 3 down, rotation 90° clockwise about point Z

Explanation:

Consider W = (2, 5)

X = (6, 5)

Y = (5, 2)

Z = (3, 2)

It was easier to name the points for the step-by-step illustration.

Step 1: Dilation of 1/2:

`W' = (1)/(2)(2, 5)\quad=\bigg(1,2(1)/(2)\bigg)\\\\X' = (1)/(2)(6, 5)\quad=\bigg(3,2(1)/(2)\bigg)\\\\Y' = (1)/(2)(5, 2)\quad=\bigg(2(1)/(2),1\bigg)\\\\Z' = (1)/(2)(3, 2)\quad=\bigg(1(1)/(2),1 \bigg)`

Step 2: Translation 5 1/2 units left and 3 units down

`W'' = \bigg(1-5(1)/(2),2(1)/(2)-3\bigg)=\bigg(-4(1)/(2),-(1)/(2)\bigg)\\\\X'' = \bigg(3-5(1)/(2),2(1)/(2)-3\bigg)=\bigg(-2(1)/(2),-(1)/(2)\bigg)\\\\Y'' = \bigg(2(1)/(2)-5(1)/(2),1-3\bigg)=\bigg(-3,-2\bigg)\\\\Z'' = \bigg(1(1)/(2)-5(1)/(2),1-3 \bigg)=\bigg(-4,-2\bigg)`

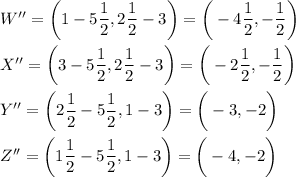
Step 3: Rotate 90° clockwise about point Z

`W''' =90^o_(Zcc)\bigg(-4(1)/(2),-(1)/(2)\bigg)=\bigg(-2(1)/(2),-1(1)/(2)\bigg)\\\\X''' = 90^o_(Zcc)\bigg(-2(1)/(2),-(1)/(2)\bigg)=\bigg(-2(1)/(2),-3(1)/(2)\bigg)\\\\Y''' = 90^o_(Zcc)\bigg(-3,-2\bigg)=\bigg(-4,-2\bigg)\\\\Z''' =90^o_(Zcc)\bigg(-4,-2\bigg)=\bigg(-4,-3\bigg)`

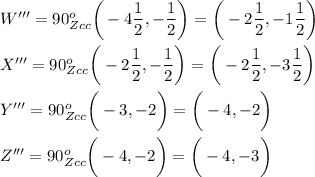
Using these three steps, you have transformed the coordinates of C into the coordinates of D.