Answer:
Explanation:
A) 2^3 * 3^3 * 5 ^ 2 * 7 ^ 1
Total factor of 378,000 including itself and 1 is
(3+1)*(3+1)*(2+1)*(1+1) = 4*4*3*2 = 96
B) Knowing its prime factorization we can solve this problem
378,000 = 378* 100
= 2 *27*7*10*10
= 2*3*3*3*7*5*2*5*2
All the above are indivisible by any number except itself and one, or are now prime numbers,from here we regroup
= 2*2*2*3*3*3*5*5*7
This can be given as 2^3 * 3^3 * 5 ^ 2 * 7 ^ 1
making the x= 0 for 2 ^ x
it becomes 2^0 * 3 ^ 3 * 5 ^ 2 * 7 ^ 1
We want the numbers of factors of the above
Therefore (0 + 1 )( 3+1)(2+1)(1+1) = 1 *4*3*2 = 24
C) From answer (B) 2^0 * 3 ^ 3 * 5 ^ 2 * 7 ^ 1 Is a factor of 378,000
And from it three the power of three and 7 are been added to know the exact time 3 and 7 can successfully divide 378,000
3+1 = 4
D) Trailing zeros are a sequence of 0's in the decimal representation (or more generally, in any positional representation) of a number, after which no other digits follow
378,000 Have three trailing zeros
Number of trailing zeros in the decimal representation of n!, the factorial of a non-negative integer n, can be determined with this formula
 +
+
Solution:
378,000!
 +
+
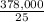 = 75,600 + 15,120 = 90,720 trailing zeros
= 75,600 + 15,120 = 90,720 trailing zeros