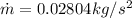Answer:
The rate of air mass flow is given as
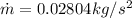
Step-by-step explanation:
The steady state energy equation is given as
![\dot{Q}-\dot{W}=\dot{m}\left[(h_2-h_1)+\left((V_1^2-V_2^2)/(2)\right)+g(z_1-z_2)\right]](https://img.qammunity.org/2021/formulas/engineering/college/f8xf8v1jvm5y2lx3y2a1ugf4qow912gpu0.png)
Here,
Q' is heat interaction per unit time with the hair dryer
W' is work interaction per unit time with the system
m' is mass flow rate into the hair dryer
Since the process is adiabatic so the value of Q' is 0 .
The elevations at inlet and outlet are same(z_1=z_2) so z_1-z_2=0
So the equation becomes
![0-\dot{W}=\dot{m}\left[(h_1-h_2)+\left((V_1^2-V_2^2)/(2)\right)+g(0)\right]\\\dot{W}=-\dot{m}\left[(h_1-h_2)+\left((V_1^2-V_2^2)/(2)\right)\right]\\\dot{W}=\dot{m}\left[(h_2-h_1)+\left((V_2^2-V_1^2)/(2)\right)\right]\\\dot{W}=\dot{m}\left[C_p(T_2-T_1)+\left((V_2^2-V_1^2)/(2)\right)\right]](https://img.qammunity.org/2021/formulas/engineering/college/tmqhstrmbkwva6v8arf8ivq0mnce9a7xe5.png)
Now the value of power is given as 1500 W so the value of W' is 1500 W
m' is to be calculated
T_2 is the temperature at the exit given as 80 C or 80+273=363K
T_1 is given as 300 K
V_1 is given as negligible so it is 0
V_2 is given as 21 m/s
C_p is given as 1.005 kJ/kgK
So the equation becomes
![\dot{W}=\dot{m}\left[C_p(T_2-T_1)+\left((V_2^2-V_1^2)/(2)\right)\right]\\1.5 kW=\dot{m}\left[1.005 kJ/kgK(363-300 )K+\left((21^2-0^2)/(2)*(1/1000)\right)\right]\\1.5=\dot{m}(53.48)\\\dot{m}=(1.5)/(53.48)\\\dot{m}=0.02804 kg/s^2](https://img.qammunity.org/2021/formulas/engineering/college/9x42y4ilhg9jo6w0s55mqg8rgqameoc7aq.png)
So the rate of air mass flow is given as