Question

An isolated conducting sphere has a 17 cm radius. One wire carries a current of 1.0000020 A into it. Another wire carries a current of 1.0000000 A out of it. How long would it take for the sphere to increase in potential by 1500 V?

Answer 1

14 ms is required to reach the potential of 1500 V.

Step-by-step explanation:

The current is measured as the amount of charge traveling per unit time. So the charge of electrons required for each current is determined as the product of current with time.

`Charge = Current * Time`

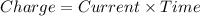
As two different current is passing at two different times, the net charge will be the different in current. So,

`\text { Charge }=(1.0000020-1.0000000) * t=2 * 10^(-6) * t`

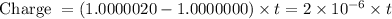
The electric voltage on the surface of cylinder can be obtained as the ratio of charge to the radius of the cylinder.

`V=(k q)/(R)`

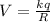
Here
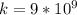`k = 9 * 10^9`, q is the charge and R is the radius. As
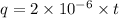`q=2 * 10^(-6) * t` and R =17 cm = 0.17 m, then the voltage will be

`V=(9 * 10^(9) * 2 * 10^(-6) * t)/(0.17)`

The time is required to find to reach the voltage of 1500 V, so

`1500 =(9 * 10^(9) * 2 * 10^(-6) * t)/(0.17)`

`\begin{aligned}&t=(1500 * 0.17)/(\left(9 * 10^(9) * 2 * 10^(-6)\right))\\&t=14.1666 * 10^(-3) s=14\ \mathrm{ms}\end{aligned}`

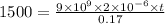
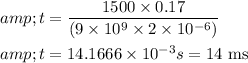
So, 14 ms is required to reach the potential of 1500 V.