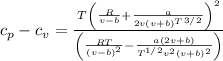Question

Derive an expression for the specific heat difference of a substance whose equation of state is 1 2 ( ) RT a P b b T ν ν ν = − − + where a and b are empirical constants.

Answer 1

Given data:

Equation of the state
`p=(RT)/(v-b)-(a)/(v(v+b) T^(1/2) )`

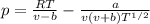
Where p = pressure of fluid, pα

T = Temperature of fluid, k

V = Specific volume of fluid
`m^(3) / k g`

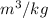
R = gas constant ,
`j/k g k`

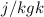
a, b = Constants

Solution:

Specific heat difference,
`\begin{array}{c}c_(p)-c_(v)=-T\left((\partial v)/(\partial T)\right)^(2) p \\\left((\partial P)/(\partial v)\right)_(r)\end{array}`

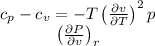
According to cyclic reaction

`\left((\ dv)/(\ dT)\right)_(p)=-(\left((\ d P)/(\ d T)\right)_(v))/(\left((\ d P)/(\ d v)\right)_(v))`

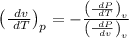
Hence specific heat difference is

`c_(p)-c_(v)=(-T\left((\ d v)/(\ d T)\right)_(p)^(2))/(\left((\ d p)/(\ dv)\right)_(v))`

Equation of state,
`p=(R T)/(v-b)-(a)/(v(v+b)^(\ 1/2))`

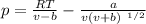
Differentiating the equation of state with respect to temperature at constant volume,

`\(\left((\ d P)/(\ d T)\right)_(v)=(R)/(v-b)-(1)/(2)- (a)/(v(v+b)^) T^{(-1)/(2)}\)`

`\begin{aligned}&\left((\ dP)/(\ dT)\right)_(V)=(R)/(v-b)+(a)/(2 v(v+b) T^(3 / 2))\end{aligned}`

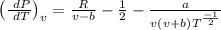
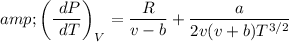
Differentiating the equation of the state with respect to volume at constant temperature.

`\(\left((\ dP)/(\ dv)\right)_(\gamma)=+(-1) * R T(v-b)^(-1-1)+(a)/(b T^(1 / 2))\left((1)/(v^(2))-(1)/((v+b)^(2))\right)\)\\\(\left((\ dP)/(\ dv)\right)_(r)=-(R T)/((v-b)^(2))+(a)/(T^(1 / 2))\left((2 v+b)/(v^(2)(v+b)^(2))\right)\)`

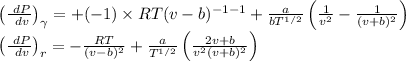
Substituting both eq (3) and eq (4) in eq (2)

We get,

`{cp{} - } c_(v)=(T\left((R)/(v-b)+(a)/(2 v(v+b) T^(3 / 2))\right)^(2))/(\left((R T)/((v-b)^(2))-(a(2 v+b))/(T^(1 / 2) v^(2)(v+b)^(2))\right))`

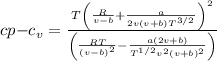
Specific heat difference equation,

`\(c_(p) -c_(v)}=(T\left((R)/(v-b)+(a)/(2 v(v+b)^(T)^(3 / 2))\right)^(2))/(\left((R T)/((v-b)^(2))-(a(2 v+b))/(T^(1 / 2) v^(2)(v+b)^(2))\right))\)`