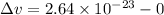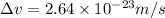Answer:
Part a)
Momentum transferred by the ball
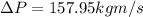
Part b)
Change in the velocity of the ball is
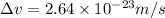
Step-by-step explanation:
Velocity of the stone just before it will strike the Earth is given as
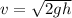
so we will have
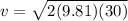
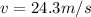
Now by momentum conservation
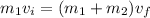
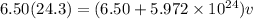
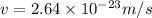
Part a)
Momentum transferred by the stone is given as
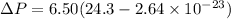
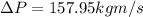
Part b)
Change in velocity of Earth