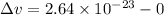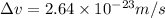Question

) A 6.50 kg rock starting from rest free-falls through a distance of 30.0 m. a. Assuming no air resistance, find the amount of momentum that is transferred from the rock to earth as it collides with earth’s surface in a perfectly inelastic collision. b. What is the change in velocity of earth as a result of this momentum change? The earth’s mass is 5.972 x 10^24 kg. Show all your work, assuming the rock–earth system is closed.

Answer 1

Part a)

Momentum transferred by the ball

`\Delta P = 157.95 kg m/s`

Part b)

Change in the velocity of the ball is

`\Delta v = 2.64 * 10^(-23) m/s`

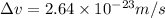
Step-by-step explanation:

Velocity of the stone just before it will strike the Earth is given as

`v = √(2gh)`

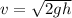
so we will have

`v = √(2(9.81)(30))`

`v = 24.3 m/s`

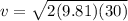
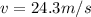
Now by momentum conservation

`m_1v_i = (m_1 + m_2) v_f`

`6.50(24.3) = (6.50 + 5.972 * 10^(24))v`

`v = 2.64 * 10^(-23) m/s`

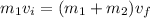
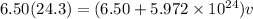
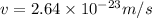
Part a)

Momentum transferred by the stone is given as

`\Delta P = 6.50(24.3 - 2.64 * 10^(-23))`

`\Delta P = 157.95 kg m/s`

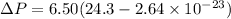
Part b)

Change in velocity of Earth

`\Delta v = 2.64 * 10^(-23) - 0`

`\Delta v = 2.64 * 10^(-23) m/s`