Question

An 80-percent-efficient pump with a power input of 20 hp is pumping water from a lake to a nearby pool at a rate of 1.5 ft3/s through a constant-diameter pipe. The free surface of the pool is 80 ft above that of the lake. Determine the mechanical power used to overcome frictional effects in piping.

Answer 1

mechanical power used to overcome frictional effects in piping is 2.37 hp

Step-by-step explanation:

given data

efficient pump = 80%

power input = 20 hp

rate = 1.5 ft³/s

free surface = 80 ft

solution

we use mechanical pumping power delivered to water is

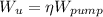`{W_(u)}= \eta {W_(pump)}` .............1

put here value

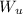`{W_(u)}` = (0.80)(20)

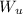`{W_(u)}` = 16 hp

and

now we get change in the total mechanical energy of water is equal to the change in its potential energy

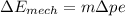`\Delta{E_(mech)} = {m} \Delta pe` ..............2

`\Delta {E_(mech)} = {m} g \Delta z`

and that can be express as

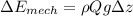`\Delta {E_(mech)} = \rho Q g \Delta z` ..................3

so

`\Delta {E_(mech)} = (62.4lbm/ft^3)(1.5ft^3/s)(32.2ft/s^2)(80ft)[(1lbf)/(32.2lbm\cdot ft/s^2)][(1hp)/(550lbf \cdot ft/s)]` ......4

solve it we get

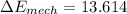`\Delta {E_(mech)} = 13.614` hp

so here

due to frictional effects, mechanical power lost in piping

we get here

`{W_(frict)} = {W_(u)}-\Delta {E_(mech)}`

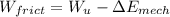
put here value

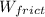`{W_(frict)}` = 16 -13.614

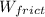`{W_(frict)}` = 2.37 hp

so mechanical power used to overcome frictional effects in piping is 2.37 hp