Question

The lowest flow in the Menominee River in July is about 40 m3/s. If the river temperature is 18°C and a power plant discharges 2 m3/s of cooling water at 80°C, what is the final river temperature after the cooling water and river have mixed?

Answer 1

`21^(\circ) \mathrm{C}` is the final river temperature after the cooling water and river have mixed.

Step-by-step explanation:

Final river temperature after mixing using energy energy balance equation

`\Delta E_{\text {River }}+\Delta E_{\text {Cooling water}}=0 \ldots \ldots(1)`

`\Delta E_{\text {River }}=Q_{\text {River}} \rho C_(P)\left(T-T_{\text {River }}\right)`

`$\Delta E_{\text {cooling water }}=Q_{\text {cooling water }} \rho C_(P)\left(T-T_{\text {Cooling water }}\right)$`

`Q_{\text {River}} \rho C_(P)\left(T-T_{\text {River }}\right)+Q_{\text {Cooling water }} \rho C_(P)\left(T-T_{\text {Cooling water }}\right)=0 \ldots \ldots .(2)`

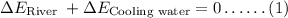
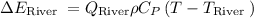
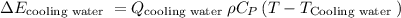
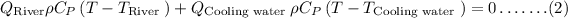
Where,
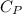`C_(P)` is specific heat at constant pressure,
`\Delta T` change in temperature,
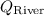`Q_{\text {River}}` is flow in the river,
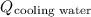`$Q_{\text {cooling water }}$`is the flow of cooling water from plant,
`T` final required temperature after mixing cooling water and river water,and,
`\rho` is density of water.

From Diagram

While substituting,

`40 \mathrm{m}^(3) / \mathrm{s} \text { for } Q_{\text {River }}`

`$2 \mathrm{m}^(3) / \mathrm{s} \quad for\quad Q_{\text {cooling water }}`

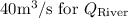
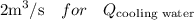
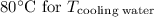`80^(\circ) \mathrm{C} \text { for } T_{\text {cooling water }}` and

`18^(\circ) \mathrm{C} \text { for } T_{\mathrm{River}}`

`Q_{\text {River}} \rho C_(P)\left(T-T_{\text {River }}\right)+Q_{\text {Cooling water }} \rho C_(P)\left(T-T_{\text {Cooling water }}\right)=0`

`40 * \rho C_(P)(T-18)+2 * \rho C_(P)(T-40)=0`

`40 *(T-18)+2 *(T-40)=0`

`T=21^(\circ) \mathrm{C}`

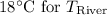
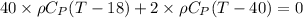
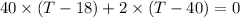
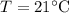
Finally, the temperature after the mixing of cool water and river is
`21^(\circ) \mathrm{C}` .