Question

a small bridge sit atop for cube shaped powers that all have the same volume. The combined volume of the four pillars is 503 how many inches long are the size of the powers explain your answer

Answer 1

60 inches long are the sides of the pillars.

Explanation:

Given : A small bridge sits atop four cube shaped pillars that all have the same volume. the combined volume of the four pillars is 500 ft cubed.

To find : How many inches long are the sides of the pillars?

Solution :

Refer the attached picture below for Clarence of question.

The volume of the cube is
`V=a^3`

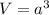
Where, a is the side.

The combined volume of the four pillars is 500 ft cubed.

The volume of each cube is given by,

`V=(500)/(4)=125\ ft^3`

Substitute in the formula to get the side,

`125=a^3`

`a=\sqrt[3]{125}`

`a=5\ ft`

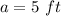
We know, 1 feet = 12 inches

So, 5 feet =
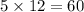`5* 12=60` inches

Therefore, 60 inches long are the sides of the pillars.