Answer:
Sally's temperature is 97.27 °F.
Explanation:
All the information given in the question tells us that the human body temperatures are normally distributed with a population's mean = 98.20°F and a standard deviation = 0.62°F.
The question gives us Sally's temperature in a z-score. We have to remember that the standard normal distribution is a particular case of a normal distribution where the mean = 0 and the standard deviation = 1.
Using the standard normal distribution, we can determine every probability associated with a normal distribution "transforming" the raw scores, coming from normally distributed data, into z-scores.
A z-score gives us the distance from the population's mean and is in standard deviation units. So, a z = 1.5 tells us that the value is 1.5 standard deviations above the mean. Conversely, a z = -1.5 tells us that the raw score is also 1.5 standard deviation from the mean, but in the opposite direction, that is, below the mean.
The formula for a z-score is as follows:
 (1)
(1)
Where
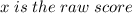 .
.
 .
.
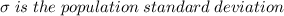 .
.
Then to find x (or the raw score, that is, Sally's temperature), we need to solve the formula (1) for it to finally solve the question.
Then
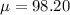 °F
°F
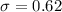 °F
°F

Thus (with no units)
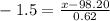
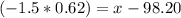
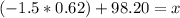
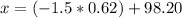
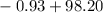
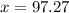 °F
°F
Thus, Sally's temperature is
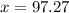 °F (rounding the answer to the nearest hundredth).
°F (rounding the answer to the nearest hundredth).