Answer:
The length of side AB is
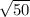 units.
units.
The length of side BC is
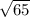 units.
units.
The length of side AC is
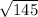 units.
units.
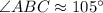 .
.
Explanation:
Given : ∆ABC has A(-3, 6), B(2, 1), and C(9, 5) as its vertices.
To find : The length of side AB is units. The length of side BC is units. The length of side AC is units. ∠ABC ≈ ° ?
Solution :
The distance formula between two point is given by,
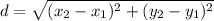
The distance between A(-3, 6) and B(2, 1) is
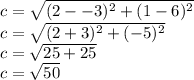
The distance between B(2, 1), and C(9, 5) is
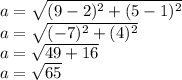
The distance between C(9, 5) and A(-3, 6) is
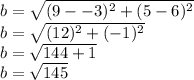
By the Law of Cosines,
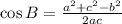
Substitute the values,
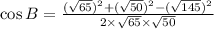
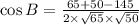
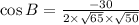
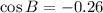
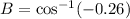
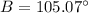
Therefore,
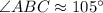 .
.