Question

∆ABC has A(-3, 6), B(2, 1), and C(9, 5) as its vertices. The length of side AB is 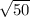units. The length of side BC is units. The length of side AC is 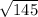units. ∠ABC ≈ °.

Answer 1

The length of side AB is
`√(50)` units.

The length of side BC is
`√(65)` units.

The length of side AC is
`√(145)` units.

`\angle ABC\approx 105^\circ`.

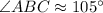Explanation:

Given : ∆ABC has A(-3, 6), B(2, 1), and C(9, 5) as its vertices.

To find : The length of side AB is units. The length of side BC is units. The length of side AC is units. ∠ABC ≈ ° ?

Solution :

The distance formula between two point is given by,

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

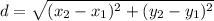
The distance between A(-3, 6) and B(2, 1) is

`c=√((2--3)^2+(1-6)^2) \\c=√((2+3)^2+(-5)^2) \\c=√(25+25)\\c=√(50)`

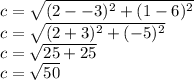
The distance between B(2, 1), and C(9, 5) is

`a=√((9-2)^2+(5-1)^2) \\a=√((-7)^2+(4)^2) \\a=√(49+16)\\a=√(65)`

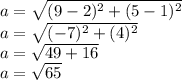
The distance between C(9, 5) and A(-3, 6) is

`b=√((9--3)^2+(5-6)^2) \\b=√((12)^2+(-1)^2) \\b=√(144+1)\\b=√(145)`

By the Law of Cosines,

`\cos B=(a^2 + c^2 -b^2)/(2ac)`

Substitute the values,

`\cos B=((√(65))^2 + (√(50))^2 - (√(145))^2)/(2* √(65)* √(50))`

`\cos B=(65+50-145)/(2* √(65)* √(50))`

`\cos B=(-30)/(2* √(65)* √(50))`

`\cos B=-0.26`

`B=\cos^(-1)(-0.26)`

`B=105.07^\circ`

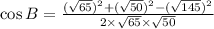
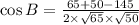
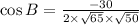
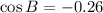
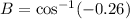
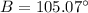
Therefore,
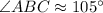`\angle ABC\approx 105^\circ`.