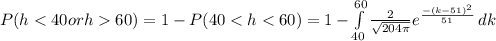Question

Suppose you flip a fair coin N times. Let random variable h be the number of heads that occur. Use the normal approximation to estimate the following probabilities. Write your answers using integrals. Do not evaluate the integrals. P(h E [495000, 505000]) given that = 100 b. P(h > 9000) given that N = 104 P(h < 40 or h > 60) given that N = 102 а. C.

Answer 1

If n = 1000000, then

`P(h E [495000, 505000]) = \int\limits^(50500)_(495000) {(2)/(√(2000000\pi)) e^{(-(k-500000)^2)/(500000) }} \, dk`

If n = 10400, then

`P(h E [495000, 505000]) = \int\limits^(50500)_(495000) {(2)/(√(2000000\pi)) e^{(-(k-500000)^2)/(500000) }} \, dk`

If N = 102, then

`P(h < 40 or h > 60) = 1-P(40<h<60) = 1-\int\limits^(60)_(40) {(2)/(√(204\pi )) e^{(-(k-51)^2)/(51) }}\, dk`

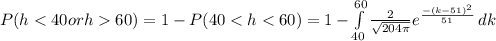
Explanation:

Since the coin is fair, then the probability that a filp is heads is 1/2. Given N tries, the amount of heads can be approximated with a Normal distribution with mean μ = N *1/2 = N/2 and standard deviation σ = √(N*1/2 * 1/2) = √N/ 2

The density function of that random variable is given by de following formula

`f_X(k) = (1)/(√(2\pi) * \sigma) e^{(-(k-\mu)^2)/(2\sigma^2) } = (2)/(√(2\pi N)) e^{(-2(k-N/2)^2)/(N) }`

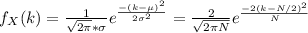
If n = 1000000, then

`P(h E [495000, 505000]) = \int\limits^(50500)_(495000) {(2)/(√(2000000\pi)) e^{(-(k-500000)^2)/(500000) }} \, dk`

If n = 10400, then

`P(h E [495000, 505000]) = \int\limits^(50500)_(495000) {(2)/(√(2000000\pi)) e^{(-(k-500000)^2)/(500000) }} \, dk`

If N = 102, then

`P(h < 40 or h > 60) = 1-P(40<h<60) = 1-\int\limits^(60)_(40) {(2)/(√(204\pi )) e^{(-(k-51)^2)/(51) }}\, dk`