Question

The planet Krypton has a mass of 4 × 1023 kg and radius of 1.1 × 106 m. What is the acceleration of an object in free fall near the surface of Krypton? The gravita- tional constant is 6.6726 × 10−11 N · m2/kg2. Answer in units of m/s2.

Answer 1

`g_K=22.0m/s^(2)`

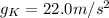
Step-by-step explanation:

From the Newton's Law of Universal Gravitation, we have that the acceleration due to gravitational force near an object of mass M, is given by:

`g=(GM)/(R^(2))`

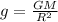
Where g is the acceleration due to gravity, G is the gravitational constant, and R is the distance between the objects.

In this case, we have the given values for planet Krypton:

`g_K=((6.6726*10^(-11)(Nm^(2))/(kg^(2)))(4*10^(23)kg))/((1.1*10^(6)m)^(2))=22.0m/s^(2)`

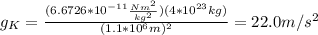
This means that the acceleration of an object in free fall near the surface of Krypton is of 22.0m/s².