Question :-
- The Area of Parallelogram is 104 units² . Its Base is 13 units . What is the Height of the Parallelogram ?
Answer :-
- Height of Parallelogram is 8 units .
Explanation :-
As per the provided information in the given question, we have been given that the Area of Parallelogram is 104 units² . Its Base is given as 13 units . And, we have been asked to calculate the Height of the Parallelogram .
For calculating the Height , we will use the Formula :-

Therefore , by Substituting the given values in the above Formula :-
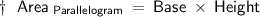
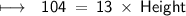
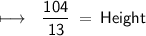
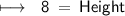

Hence :-
- Height of Parallelogram = 8 units .

Additional Information :-
![\begin{gathered} \begin{gathered} \begin{gathered}\begin{gathered}\boxed{\begin{array}{c} \\ \underline{ { \textbf {\textsf \red{ \dag \: \: More \: Formulas \: \: \dag}}}} \\ \\ \\ \footnotesize \bigstar \: \bf{Area \: _(Square) = Side * Side} \\ \\ \\ \footnotesize\bigstar \: \bf{Area \: _(Rectangle) = Lenght * Breadth} \\ \\ \\ \footnotesize \bigstar \: \bf{Area \: _(Triangle) = (1)/(2) * Base * Height } \\ \\ \\ \footnotesize \bigstar \: \bf{Area \: _(Parallelogram) = Base * Height} \\ \\ \\ \footnotesize \bigstar \: \bf{Area \: _(Trapezium) = (1)/(2) * [ \: A + B \: ] * Height } \\ \\ \\ \footnotesize \bigstar \: \bf {Area \: _(Rhombus) = (1)/(2) * Diagonal \: 1 * Diagonal \: 2}\end{array}}\end{gathered}\end{gathered} \end{gathered} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/i3v9pmxymjkh4akyzni9sus46vklqyzr7c.png)