Question

The two rectangular prisms are similar. What is the volume of the larger rectangular prism?

Answer 1

The answer is 1620cm squared!

Answer 2

The question is missing the figure which is attached below.

Answer:

1620 cm³

Explanation:

Given:

The two prisms are similar.

Volume of the smaller prism (V₁) = 60 cm³

Length of the smaller prism (l₁) = 5 cm

Length of the larger prism (l₂) = 15 cm

Now, we know that, for similar figures, the dimensions of the figure are in proportion to each other. Therefore,

`(l_2)/(l_1)=(b_2)/(b_1)=(h_2)/(h_1)=k(constant)\\\\Where,\\b_1,b_2\to\ widths\ of smaller\ and\ larger\ prisms\ respectively\\\\h_1,h_2\to\ heights\ of\ smaller\ and\ larger\ prisms\ respectively`

`(l_2)/(l_1)=(15\ cm)/(5\ cm)=3\\\\\therefore\ k=3`

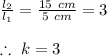
This means that, the smaller figure is dilated by a scale factor of 3.

Hence,
`l_2=3l_1,b_2=3b_1,h_2=3h_1`

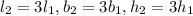
Volume of smaller prism is given as:

`V_1=l_1b_1h_1\\\\l_1b_1h_1=60\ cm^3`

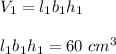
Volume of larger prism is given as;

`V_2=l_2b_2h_2\\\\V_2=3l_1* 3b_1* 3h_1\\\\V_2=27(l_1 b_1h_1)\\\\V_2=27* 60=1620\ cm^3\ \ \ \ [\because\ l_1b_1h_1=60\ cm^3]`

Therefore, the volume of the larger rectangular prism is 1620 cm³.