The question is missing the figure which is attached below.
Answer:
1620 cm³
Explanation:
Given:
The two prisms are similar.
Volume of the smaller prism (V₁) = 60 cm³
Length of the smaller prism (l₁) = 5 cm
Length of the larger prism (l₂) = 15 cm
Now, we know that, for similar figures, the dimensions of the figure are in proportion to each other. Therefore,

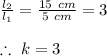
This means that, the smaller figure is dilated by a scale factor of 3.
Hence,
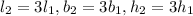
Volume of smaller prism is given as:
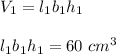
Volume of larger prism is given as;
![V_2=l_2b_2h_2\\\\V_2=3l_1* 3b_1* 3h_1\\\\V_2=27(l_1 b_1h_1)\\\\V_2=27* 60=1620\ cm^3\ \ \ \ [\because\ l_1b_1h_1=60\ cm^3]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9865c5hp3cp8ukllxyffybkpx7lhz1zks1.png)
Therefore, the volume of the larger rectangular prism is 1620 cm³.