Step-by-step explanation:
Specifications for dimension #11 are
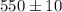
This means, mean is 550, and margin of error on each side is 10
Sample size is n= 5
Standard Deviation
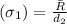
Where
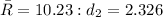 (d2 is a constant dependant on sample size)
(d2 is a constant dependant on sample size)
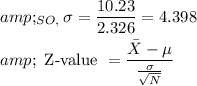
Here, 547.9 is the process mean and 550 is population mean, subgroup size is 5 and standard deviation in each subgroup is 4.398
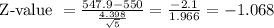
p-value corresponding to z- value of -1.068 is 0.1446
So, 14.46% area on each side would be outside the range -1.068, +1.068
Total % of shaft outside the specifications are: 14.46*2 =28.92%