Answer:
It took
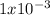 seconds for batman's hand to stop moving.
seconds for batman's hand to stop moving.
Step-by-step explanation:
Newton' s second law is defined as:
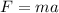 (1)
(1)
Where m is the mass and a is the acceleration.
But it is known that the acceleration is defined as follow by the kinematic equation that corresponds to a Uniformly Accelerated Rectilinear Motion.
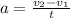 (2)
(2)
Where
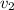 is the final velocity and
is the final velocity and
 is the initial velocity
is the initial velocity
The initial velocity of the fist will be zero (
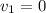 ) since it starts from a state of rest.
) since it starts from a state of rest.
Then, equation 2 can be replaced in equation 1
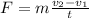 (3)
(3)
Therefore, t can be isolated from equation 3
 (4)
(4)
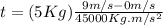
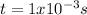
Hence, it took
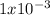 seconds for batman's hand to stop moving.
seconds for batman's hand to stop moving.