Question

Batman is fighting superman. He throws his 5 kg fist at superman with a speed of 9 m/s. Superman stops the punch with a force of 45,000 N. How much time did it take for batman's hand to stop moving?

Answer 1

1 × 10^-3 s.

Step-by-step explanation:

Given:

Mass = 5 kg

V = 9 m/s

Force = 45000 N

Using Newton's law,

Force = mass × acceleration

= (mass × velocity)/time

45000 = (5 × 9)/time

Time = 1 × 10^-3 s.

Answer 2

It took
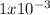`1x10^(-3)` seconds for batman's hand to stop moving.

Step-by-step explanation:

Newton' s second law is defined as:

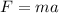`F = ma` (1)

Where m is the mass and a is the acceleration.

But it is known that the acceleration is defined as follow by the kinematic equation that corresponds to a Uniformly Accelerated Rectilinear Motion.

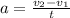`a = (v_(2)-v_(1))/(t)` (2)

Where
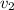`v_(2)` is the final velocity and
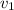`v_(1)` is the initial velocity

The initial velocity of the fist will be zero (
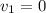`v_(1) = 0`) since it starts from a state of rest.

Then, equation 2 can be replaced in equation 1

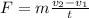`F = m(v_(2)-v_(1))/(t)` (3)

Therefore, t can be isolated from equation 3

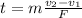`t = m(v_(2)-v_(1))/(F)` (4)

`t = (5Kg)(9m/s-0m/s)/(45000Kg.m/s^(2))`

`t = 1x10^(-3)s`

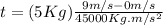
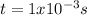
Hence, it took
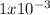`1x10^(-3)` seconds for batman's hand to stop moving.