Option B:
Equation of a line is
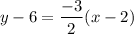
Solution:
Equation of a parallel line:
3x + 2y = 5
2y = –3x + 5
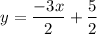
Slope of this line,
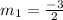
If two lines are parallel, then slopes of their lines are equal.


The line passes through the point (2, 6)
Point-slope formula:

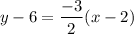
This is the equation of the line.
Option B is the correct answer.