x = 10.22 in
Solution:
Width of the figure = x in
Length of the figure = (2x + 5) in
Area of the figure = 260 in²
To find the value of x:
Area of the figure = length × width
length × width = 260
(2x + 5) × x = 260
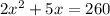
Subtract 260 from both sides of the equation.
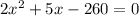
Factor the above quadratic expression.
Quadratic equation formula:
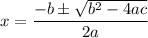
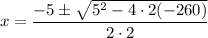
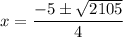
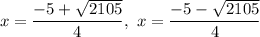
x = 10.22, x = –12.72006
Dimension of the figure cannot be measured in negative terms.
Hence x = 10.22 in.