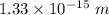Answer:
The wavelength of the proton will be
Step-by-step explanation:
Given the speed of the proton is
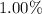 of speed of light.
of speed of light.
And the mass of the proton is
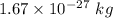 ..
..
We need to find the wavelength of moving proton.
As we know the speed of the light
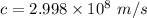
So, speed of the proton will be
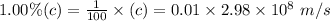
Now, we will use De Broglie's Equation to find out wavelength..
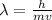
Where
 is the wavelength
is the wavelength
 is the Planck's constant
is the Planck's constant
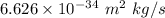
 is the mass in kg
is the mass in kg
 is the speed in m/s
is the speed in m/s
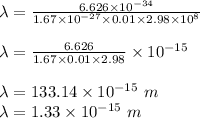
So, the wavelength of the proton will be