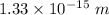Question

(1 points) Find the wavelength of a proton moving at 1.00% of the speed of light. The mass of a proton is 1.67 \times 10^{-27} ~\text{kg}1.67×10 ​−27 ​​ kg.

Answer 1

The wavelength of the proton will be
`1.33* 10^(-15)\ m`

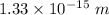
Step-by-step explanation:

Given the speed of the proton is
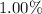`1.00 \%` of speed of light.

And the mass of the proton is
`1.67 * 10^(-27)\ kg`..

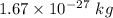We need to find the wavelength of moving proton.

As we know the speed of the light
`c=2.998* 10^8\ m/s`

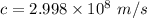
So, speed of the proton will be

`1.00 \%(c)=(1)/(100)* (c)=0.01* 2.98* 10^8\ m/s`

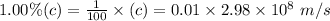
Now, we will use De Broglie's Equation to find out wavelength..

`\lambda =(h)/(mv)`

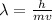
Where

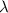`\lambda` is the wavelength

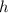`h` is the Planck's constant
`6.626* 10^(-34)\ m^2\ kg / s`

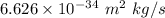
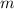`m` is the mass in kg

`v` is the speed in m/s

`\lambda=(6.626* 10^(-34))/(1.67 * 10^(-27)* 0.01* 2.98* 10^8)\\ \\\lambda=(6.626)/(1.67* 0.01* 2.98)* 10^(-15)\\ \\\lambda=133.14* 10^(-15)\ m\\\lambda=1.33* 10^(-15)\ m`

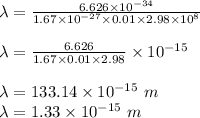
So, the wavelength of the proton will be
`1.33* 10^(-15)\ m`