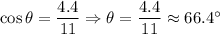Question

Help with trig plz 70 pts. plz give a legit answer no guessing

Answer 1

See explanation

Explanation:

Use trigonometric functions to solve your problems:

`\cos \theta=\frac{\text{Adjacent leg}}{\text{Hypotenuse}}\\ \\\sin \theta=\frac{\text{Opposite leg}}{\text{Hypotenuse}}\\ \\\tan \theta=\frac{\text{Opposite leg}}{\text{Adjacent leg}}\\ \\\cot \theta=\frac{\text{Adjacent leg}}{\text{Opposite leg}}`

Q1. From the diagram,

Adjacent leg AC = 12

Hypotenuse AB = 13

Then
`\cos \theta =(12)/(13)\Rightarrow \theta =\arccos (12)/(13)\approx 22.6^(\circ)`

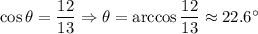
Q2. From the diagram,

Adjacent leg AC = 13

Opposite leg BC = 4

Then
`\tan \theta =(4)/(13)\Rightarrow \theta =\arctan (4)/(13)\approx 17.1^(\circ)`

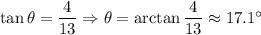
Q3. From the diagram,

Adjacent leg AC = 6

Hypotenuse AB = 9

Then
`\cos \theta =(6)/(9)\Rightarrow \theta =\arccosn (6)/(9)\approx 48.2^(\circ)`

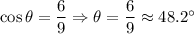
Q4. From the diagram,

Adjacent leg AC = 10

Opposite leg BC = 11.9

Then
`\tan \theta =(11.9)/(10)\Rightarrow \theta =\arctan (11.9)/(10)\approx 50^(\circ)`

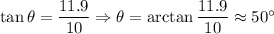
Q5. From the diagram,

Adjacent leg BC = 14

Opposite leg AC = 7.7

Then
`\tan \theta =(7.7)/(14)\Rightarrow \theta =\arctan (7.7)/(14)\approx 28.8^(\circ)`

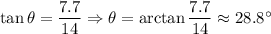
Q6. From the diagram,

Adjacent leg BC = 4

Hypotenuse AB = 5

Then
`\cos \theta =(4)/(5)\Rightarrow \theta =\arccosn (4)/(5)\approx 36.9^(\circ)`

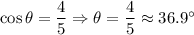
Q7. From the diagram,

Adjacent leg BC = 4.4

Hypotenuse AB = 11

Then
`\cos \theta =(4.4)/(11)\Rightarrow \theta =\arccosn (4.4)/(11)\approx 66.4^(\circ)`