Answer:
Part 11) The vertex is the point (4,32)
Part 12) The vertex is the point (1,-5)
Part 13) The vertex is the point (-2,5)
Part 14) The vertex is the point (-1,-1)
Part 15) The vertex is the point (1,8)
Part 16) The vertex is the point (3,-26)
Part 17) The vertex is the point (-5,-32)
Explanation:
Part 11) we have
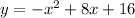
we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form
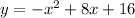
Factor -1
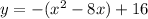
Complete the square
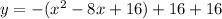
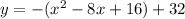
Rewrite as perfect squares

The vertex is the point (4,32)
Part 12) we have

we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form

Factor 3
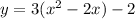
Complete the square


Rewrite as perfect squares
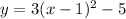
The vertex is the point (1,-5)
Part 13) we have
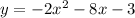
we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form
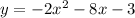
Factor -2
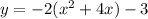
Complete the square
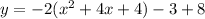
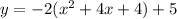
Rewrite as perfect squares
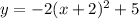
The vertex is the point (-2,5)
Part 14) we have
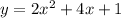
we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form
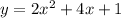
Factor 2

Complete the square

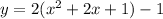
Rewrite as perfect squares
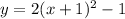
The vertex is the point (-1,-1)
Part 15) we have
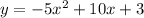
we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form
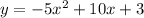
Factor -5
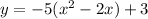
Complete the square
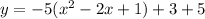
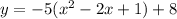
Rewrite as perfect squares
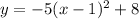
The vertex is the point (1,8)
Part 16) we have

we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form

Factor 3
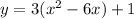
Complete the square
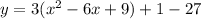

Rewrite as perfect squares

The vertex is the point (3,-26)
Part 17) we have
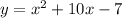
we know that
The quadratic equation written in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex
Convert to vertex form
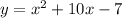
Complete the square
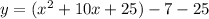

Rewrite as perfect squares
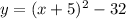
The vertex is the point (-5,-32)